线性回归 - MLLearning

线性回归是基本的监督机器学习算法，用于模拟一个因变量（目标变量）与一个或多个自变量（解释变量）之间的线性关系。

这种方法在统计学、机器学习和许多科学领域都非常常用，用于数据分析和预测建模。

面试题详解

请描述一下线性回归算法的原理?

线性回归的核心目标是找到一个线性方程，该方程最好地描述了自变量和因变量之间的关系。

aaa

线性回归主要分为。

简单线性回归

模型只包含一个自变量和一个因变量，形式为

$\(y = \beta_0 + \beta_1x + \epsilon$\)

其中 $y$ 是因变量，$x$ 是自变量，$\beta_0$ 是截距，$\beta_1$ 是斜率，而 $\epsilon$ 是误差项。

多元线性回归

模型包含多个自变量，形式为

$\(y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_nx_n + \epsilon$\)

其中 $x_1,x_2,…,x_n$ 是自变量。

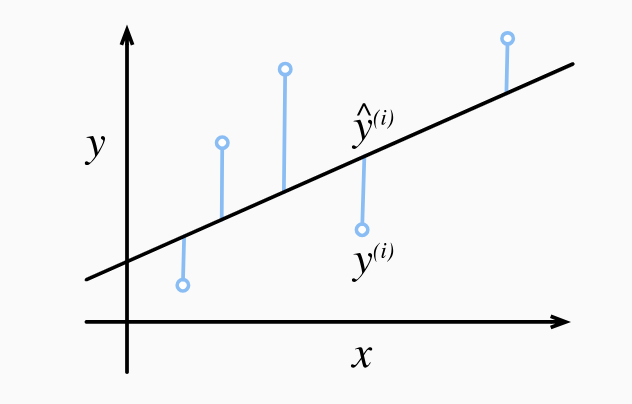
线性回归的优化目标是找到一组参数（即斜率和截距），使得模型预测的输出与实际数据之间的误差最小。这个误差通常通过一个损失函数来量化，线性回归中最常用的损失函数是均方误差（MSE）。

稀疏模型

# 首先，需要导入必要的库
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.datasets import make_regression
from sklearn.metrics import mean_squared_error, r2_score

# 生成一些用于回归分析的数据
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)

# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建线性回归模型实例
lr_model = LinearRegression()

# 用训练集数据训练（拟合）模型
lr_model.fit(X_train, y_train)

# 用拟合好的模型预测测试集的响应变量
y_pred = lr_model.predict(X_test)

# 计算均方误差和决定系数
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

# 打印均方误差和决定系数
print(f"Mean Squared Error (MSE): {mse}")
print(f"R-squared (R2): {r2}")

# 如果需要查看模型参数，可以如下打印
print(f"Coefficients: {lr_model.coef_}")
print(f"Intercept: {lr_model.intercept_}")

# Mean Squared Error (MSE): 104.20222653187027
# R-squared (R2): 0.9374151607623286
# Coefficients: [44.24418216]
# Intercept: 0.09922221422587718

aaa

如何理解线性回归中的“线性”概念？

在统计学和机器学习中，线性回归模型的 “线性” 主要指的是模型参数与因变量之间的关系是线性的。

在传统意义上，线性回归确实是指模型产生直线（在二维空间）或平面（在更高维度的空间）。然而，通过变换自变量，可以使线性回归模型适用于曲线关系的建模。这种方法称为线性化或线性回归的非线性变换。

例如，假设你有一个因变量 Y 和一个自变量 X，并且你怀疑它们之间的真实关系是二次的 $Y=\beta_0+\beta_1X+\beta_2X^2+ϵ$。虽然这个模型是非线性的，但你可以通过引入一个新的自变量 $X^2=X_2$，将其转化为线性模型：

$Y = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \epsilon$

在这种情况下，虽然关于 X 的原始关系是曲线的，但转换后的模型对于 $X_1$ 和 $X_2$ 仍然是线性的。通过这种方法，你可以使用线性回归来拟合多种曲线关系，例如二次关系、指数关系、对数关系等。

线性回归算法的基本假设是什么？

线性回归模型的有效性基于几个关键假设，满足这些假设可以确保模型结果的最优和可靠。

线性关系：自变量（解释变量）和因变量（响应变量）之间应存在线性关系。
同方差性：不同观测点的误差项应具有相同的方差。如果方差随着自变量的增加而增加或减少，这称为异方差性，可能需要对模型进行调整。
独立性：观测点之间应相互独立。在时间序列数据中，违反独立性的现象称为自相关。
误差项的正态分布：为了使得回归分析中的统计测试有效，误差项应当呈正态分布。当样本量足够大时，根据中心极限定理，即使误差项的分布不是正态的，估计的参数仍然是有效的。
无多重共线性：模型中的自变量应相互独立，不存在完全或高度的线性相关。多重共线性会导致参数估计的不稳定和解释的困难。
误差项的零均值：对于所有的观测值，误差项的平均值应该为零。
无误差项的自相关：在任何两个不同的观测值之间，误差项应该是不相关的。

违反这些假设可能会导致模型效果不佳。此外，线性回归对异常值非常敏感，可能会显著影响模型系数和预测的准确性。

什么是残差？

线性回归算法中的残差是一个关键概念，它指的是在回归模型中，每个观测值与模型预测值之间的差异。

残差是衡量线性回归模型拟合度的重要工具，它们为理解和改进模型提供了重要的洞察。

具体来说，假设你有一组数据点 $(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$，其中 $x_i$ 是解释变量（或自变量），而 $y_i$ 是响应变量（或因变量）。在线性回归中，我们试图找到一个线性关系（通常是一条直线），它尽可能好地描述 x 与 y 之间的关系。这条直线可以用方程 $y = \beta_0 + \beta_1x $ 表示，其中 $\beta_0$ 是截距， $\beta_1$ 是斜率。

对于每个数据点 $i$，线性回归模型预测的值是 $\hat{y}_i = \beta_0 + \beta_1 x_i$，残差 $e_i$ 就是实际观测值 $y_i$ 和预测值 $\hat{y}_i$ 之间的差异，即 $e_i = y_i - \hat{y}_i$

残差有以下几个重要特性：

平均值为零：理想情况下，残差的平均值应接近于零，这表明模型没有系统性偏差。
随机分布：好的线性回归模型的残差应随机分布，没有可辨认的模式或趋势。
恒定的方差（同方差性）：对于所有的 x 值，残差的方差应该是恒定的。

线性回归的评估指标有哪些？

线性回归模型的评估指标主要衡量的是模型预测值与实际观测值的接近程度，常用的评估指标包括：

均方误差 (MSE, Mean Squared Error)

均方误差是每个预测值与实际值之差的平方的平均值。

$\(MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2$\)

均方根误差 (RMSE, Root Mean Squared Error)

MSE 的平方根，为了保持误差单位与原始数据一致。

$$ RMSE = \sqrt{MSE}$$

平均绝对误差 (MAE, Mean Absolute Error)

计算预测值与实际值之间的绝对值的平均。

\[MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i|\]
决定系数（R², Coefficient of Determination）

表征模型对数据变异性的解释程度，它的取值范围为 0 到 1。R² 值接近 1 表示模型解释了数据中的大部分变异性，而接近 0 的值表示模型没有解释太多。换句话说，越接近1，模型的性能越好。

$\(R² = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}$\)

其中 $\bar{y}$ 是 $y_i$ 的平均值

调整 R² (Adjusted R²)

考虑了自变量数量对 R² 的影响，更适用于比较包含不同数量自变量的模型。

$\(Adjusted R² = 1 - (1 - R²) \frac{n-1}{n-p-1}$\)，其中 $n$ 是样本数量，$p$ 是模型中自变量的数量。

这些指标各有优势和局限性，选择合适的评估指标通常取决于具体的应用场景和模型的目的。例如，如果对误差的大小非常敏感，可以使用RMSE，如果要衡量模型解释数据变异性的能力，则使用 R² 或调整 R²。

在实际应用中，通常会结合多个指标来全面评估线性回归模型的性能。

什么是最小二乘法？

最小二乘法是一种数学优化技术，用于确定一组参数的值，这些参数定义了一个函数，以便该函数最好地拟合一组数据。

它通过最小化观测值与模型预测值之间差的平方和来实现这一点，通常用于线性回归分析。

具体来说，在线性回归的上下文中，假设有一组观测数据 $(x_1,y_1),(x_2,y_2),...,(x_n,y_n)$，我们希望找到一个线性函数 $y = \beta_0 + \beta_1x$ 来描述变量 x 和 y 之间的关系。最小二乘法会寻找系数 $\beta_0$ 和 $\beta_1 $，以使下面的损失函数最小化：

$S = \sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 = \sum_{i=1}^{n} (y_i - (\beta_0 + \beta_1 x_i))^2$

为了找到 S 的最小值，我们需要对 $β_0$ 和 $β_1$ 进行偏导，并将导数设置为零，得到两个方程：

\[\frac{\partial S}{\partial \beta_0} = -2 \sum_{i=1}^{n} (y_i - \beta_0 - \beta_1 x_i) = 0 \]

\[\frac{\partial S}{\partial \beta_1} = -2 \sum_{i=1}^{n} (y_i - \beta_0 - \beta_1 x_i) x_i = 0\]

解上述方程组可以得到 $β_0$ 和 $β_1$ 的最优解，即最小化残差平方和的参数值。

\[\beta_0 = \bar{y} - \beta_1 \bar{x} \]

\[\beta_1 = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^{n}(x_i - \bar{x})^2}\]

其中，$\bar{x} $ 是 $x_i$ 的平均值，$\bar{y}$ 是 $ y_i$ 的平均值。

通过解这个方程组，我们可以得到线性回归模型参数的闭式解，通常称为正规方程的解。

下面是调用 sklearn库实现线性回归算法的示例，其算法内容使用了最小二乘法的原理。

from sklearn.linear_model import LinearRegression
import numpy as np

# 示例数据
x = np.array([0, 1, 2, 3, 4]).reshape(-1, 1)  # 自变量（特征）
y = np.array([1, 3, 7, 13, 21])              # 因变量（目标）

# 创建一个线性回归模型的实例
model = LinearRegression()

# 训练模型
model.fit(x, y)

# 获取系数和截距
a = model.coef_[0]
b = model.intercept_

print(f"线性模型的系数: a = {a}, b = {b}")

#线性模型的系数: a = 4.999999999999999, b = -0.9999999999999982

你能不调用库，手动实现线性回归算法吗？

当然可以，在这里，我们使用基本的数学和线性代数知识来实现。

import numpy as np

# 示例数据
x = np.array([0, 1, 2, 3, 4])
y = np.array([1, 3, 7, 13, 21])

# 计算x和y的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

# 计算系数 a
numerator = sum((x - x_mean) * (y - y_mean))
denominator = sum((x - x_mean)**2)
a = numerator / denominator

# 计算截距 b
b = y_mean - a * x_mean

print(f"线性模型的系数: a = {a}, b = {b}")
#线性模型的系数: a = 5.0, b = -1.0

在这个实现中，我们首先计算了 x 和 y 的均值。然后，我们计算了系数 a 的分子和分母，最后计算出了截距 b。

这个实现遵循了最小二乘法的基本原理，适用于简单的线性回归情况。对于更复杂的数据或模型，可能需要使用更高级的技术和方法。

线性回归算法的优缺点？

线性回归算法是预测分析和统计建模中最基础和广泛使用的技术之一。

它具有如下优点：

简单性和解释性强

线性回归模型简单易懂，模型的输出易于解释，使它成为一个良好的起点分析工具。

计算效率高

线性回归算法计算上不复杂，可以快速地适应数据变化。

模型形式灵活

线性回归可以轻松处理多变量的情况，且可以使用变换来处理非线性关系。

基础性

它是许多其他算法的基础，理解了线性回归可以更容易地学习和理解更复杂的算法。

关系量化

线性回归不仅可以预测输出，还可以量化输入变量与输出之间的关系强度。

易于实现和训练

大多数编程语言和统计软件都有线性回归的实现，易于训练和部署

它具有如下缺点

对异常值敏感

线性回归对异常值非常敏感，少量的异常值可以显著影响模型的性能。

多重共线性问题

当数据中的独立变量高度相关时，线性回归的性能会下降，有时会导致不稳定的模型估计。

过度拟合风险

如果不适当地处理（例如，不使用正则化），线性回归可能会过度拟合训练数据。

外推风险

线性回归模型对于数据集范围之外的预测可能不可靠。

线性回归中的下溢和上溢现象分别指什么？

在线性回归模型中，下溢（Underflow）和上溢（Overflow）现象通常涉及浮点数的数值范围和精度。

下溢 (Underflow)

现象：下溢发生在数值太小，无法表示为一个非零的浮点数时。在线性回归模型中，这可能发生在计算很小的概率或者在应用对数变换时。
避免方法
使用对数概率而不是直接概率，比如在处理乘积概率时使用对数和。
选择合适的数据表示格式，如双精度浮点数，以增加表示范围。
对数据进行规范化或标准化，使其处于合理的数值范围内。

上溢 (Overflow)

现象：上溢是指数值太大，超出了计算机浮点数表示的范围，通常结果会被近似为无穷大。在线性回归中，当计算的预测值或某些参数在数值上变得非常大时可能会发生。
避免方法
对特征进行规范化或标准化，以减少数值的规模。
使用正规化技术（如岭回归或Lasso）来减少系数的大小。
使用更高精度的数据类型。

对于线性回归模型，选择合适的数据预处理方法和数值计算技术是至关重要的。例如，在逻辑回归中，通常使用对数几率或对数损失函数来防止数值问题，而在线性回归中，规范化输入特征的范围可以减少数值计算的不稳定性。

什么是岭回归和Lasso回归？

岭回归和Lasso回归是线性回归的两种扩展，它们都通过引入正则化项来处理某些特定类型的数据问题，特别是在存在多重共线性或希望进行变量选择时。

岭回归

岭回归通过在损失函数中加入一个正则项（惩罚项）来减少模型复杂度，防止过拟合。在岭回归中，正则项是系数的平方和，这种方法特别适用于解决具有多重共线性的数据集（即输入变量高度相关）

岭回归的目标是最小化以下目标函数。

\[\text{Minimize: } \left\{ \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{p} \beta_j^2 \right\}\]

其中

$y_i$ 是观测值，
$\hat{y}_i$ 是预测值，
$\beta_j$ 是回归系数，
$λ$ 是正则化参数（也称为岭参数），它控制了惩罚的强度。

正则化参数 λ 的大小决定了对回归系数的约束程度。当 λ 很大时，约束强度大，系数趋于零，从而减少了模型的复杂度和过拟合的风险。然而，如果 λ 设置得过大，可能会导致欠拟合。

from sklearn.linear_model import Ridge
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 生成模拟数据集
X, y = make_regression(n_samples=100, n_features=2, noise=0.1, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建岭回归模型实例，alpha是正则化强度
ridge_model = Ridge(alpha=1.0)

# 拟合训练数据
ridge_model.fit(X_train, y_train)

# 获取系数和截距
coefficients = ridge_model.coef_
intercept = ridge_model.intercept_

# 在测试集上进行预测
y_pred = ridge_model.predict(X_test)

# 计算测试集上的均方误差
mse = mean_squared_error(y_test, y_pred)

# 打印系数、截距和均方误差
print(f'Coefficients: {coefficients}')
print(f'Intercept: {intercept}')
print(f'Mean Squared Error: {mse}')

# Coefficients: [86.36361962 73.19145993]
# Intercept: -0.18073404705297236
# Mean Squared Error: 1.8170341126687597

Lasso 回归

Lasso 回归也是一种正则化线性回归的方法，但与岭回归不同的是，它使用的是系数的绝对值之和作为正则项，这有助于在模型中产生稀疏性，即使得某些回归系数变为零，从而实现变量的选择。

$\text{Minimize: } \left\{ \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \lambda \sum_{j=1}^{p} |\beta_j| \right\}$

其中各项的含义与岭回归中相同，但这里 λ 的作用是对系数的大小进行约束，而不是平方。

由于 Lasso 回归倾向于产生稀疏模型，因此它可以用作特征选择的工具，以确定最重要的变量。

Lasso回归在某些情况下可以极大地简化模型，使模型更易于解释。

from sklearn.linear_model import Lasso
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# 生成模拟数据集
X, y = make_regression(n_samples=100, n_features=2, noise=0.1, random_state=42)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 创建Lasso回归模型实例，alpha是正则化强度
lasso_model = Lasso(alpha=1.0)

# 拟合训练数据
lasso_model.fit(X_train, y_train)

# 获取系数和截距
coefficients = lasso_model.coef_
intercept = lasso_model.intercept_

# 在测试集上进行预测
y_pred = lasso_model.predict(X_test)

# 计算测试集上的均方误差
mse = mean_squared_error(y_test, y_pred)

# 打印系数、截距和均方误差
print(f'Coefficients: {coefficients}')
print(f'Intercept: {intercept}')
print(f'Mean Squared Error: {mse}')


# Coefficients: [86.47584465 73.0952485]
# Intercept: -0.16459743403035532
# Mean Squared Error: 1.8474490450340102

对比

惩罚项：岭回归使用 L2 范数作为惩罚项，Lasso 回归使用 L1 范数。
变量选择：Lasso 可以自动进行变量选择并输出一个更简洁的模型，而岭回归则会收缩参数，但不会将它们设置为零。
解的唯一性：岭回归通常会有唯一解，因为 L2 惩罚项确保了正则化项是严格凸函数，Lasso 回归可能有多个解，尤其是当特征数量大于观测数量时。

选择使用岭回归还是 Lasso 回归取决于数据集的特点及分析者对模型稀疏性的需求。

什么是弹性网络正则化？

弹性网络正则化（Elastic Net Regularization）是一种同时结合了 L1 和 L2 正则化的线性回归方法。

它在回归模型中添加了两个不同的惩罚项（正则项），从而兼具岭回归和Lasso回归的优点。弹性网络旨在综合 L1正则化的变量选择功能和 L2 正则化处理多重共线性的能力。

在数学上，弹性网络正则化的目标函数是：

\[ \text{Minimize: } \left\{ \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \lambda_1 \sum_{j=1}^{p} |\beta_j| + \lambda_2 \sum_{j=1}^{p} \beta_j^2 \right\} \]

其中

这里：

$y_i$ 是观测值
$\hat{y}_i$ 是预测值
$\beta_j$ 是回归系数
$\lambda_1 $ 控制 L1惩罚的强度，即系数的绝对值之和
$\lambda_2$ 控制 L2 惩罚的强度，即系数的平方和

弹性网络正则化特别适用于以下几种情况

当有许多特征时，这些特征中的大部分对目标变量只有微弱的相关性。
当不同的特征之间存在高度相关性时，即存在多重共线性。
当特征数量超过样本数量时，即 p>n 的情况。

import numpy as np
from sklearn.linear_model import ElasticNet
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Generate synthetic data
np.random.seed(0)
X = np.random.rand(100, 2)  # Two features
y = 2 * X[:, 0] + 3 * X[:, 1] + np.random.rand(100)  # Linear relationship with noise

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create and train the ElasticNet model
elastic_net = ElasticNet(alpha=1, l1_ratio=0.5)  # alpha controls the strength of regularization, l1_ratio balances L1 and L2
elastic_net.fit(X_train, y_train)

# Make predictions
y_pred = elastic_net.predict(X_test)

# Calculate the Mean Squared Error (MSE) to evaluate the model
mse = mean_squared_error(y_test, y_pred)
print(f"Mean Squared Error: {mse}")

#Mean Squared Error: 1.2168567730283397

aaa

Keys	Action
`?`	Open this help
`n`	Next page
`p`	Previous page
`s`	Search