什么是层次聚类?
层次聚类算法中有哪些链接方法?
层次聚类的方法有哪些?
在层次聚类中,"树状图"(Dendrogram)是什么,它如何帮助我们理解数据?
层次聚类算法的优缺点?
层次聚类的局限性和改进方法?
面试题详解
什么是层次聚类
层次聚类算法(Hierarchical Clustering)是一种常用的聚类分析方法,旨在将数据点划分为具有层次结构的群集。它通过基于相似性度量合并或拆分集群来创建集群的层次结构。
层次聚类主要有两种类型:
- 凝聚的层次聚类(Agglomerative Hierarchical Clustering)
- 分裂的层次聚类(Divisive Hierarchical Clustering)。
凝聚的层次聚类
凝聚层次聚类是最常见的层次聚类类型,用于根据对象的相似性将对象分组到聚类中。
它也称为 AGNES(聚合嵌套),这是一种 “自下而上” 的方法: 每个观察都从自己的集群开始,当一个集群向上移动时,成对的集群就会合并。

算法步骤
- 开始状态:每个数据点作为一个单独的群集。
- 迭代过程:在每一步中,最相似(或最近)的群集被合并。
- 结束条件:所有数据点被合并成一个单一的群集,或者达到了预设的群集数量。
有多种方法可以测量簇之间的距离以确定聚类规则,它们通常称为链接方法。
一些常见的链接方法有:
- 完全链接:两个簇之间的距离定义为每个簇中两点之间的最长距离。
- 单链接:两个簇之间的距离定义为每个簇中两点之间的最短距离。
- 平均链接:两个簇之间的距离定义为一个簇中的每个点到另一个簇中的每个点之间的平均距离。
- 质心链接:找到簇1的质心和簇2的质心,然后计算两者之间的距离。
树状图
树状图(Dendrogram)是一种图形化的表示方式,用于展示数据的层次聚类结果。
它是层次聚类算法中的一个关键组成部分,因为它提供了一种直观的方式来理解数据点是如何逐步组合成更大的群集的。
其中纵轴表示距离或相似度。
分裂的层次聚类
分裂的层次聚类是一种自上而下的聚类方法,我们将所有观察值分配给单个聚类,然后将该聚类划分为两个最不相似的聚类。最后,我们对每个聚类进行递归处理,直到每个观察都有一个聚类。所以这种聚类方法与聚合聚类完全相反。

算法步骤
- 开始状态:所有数据点在一个群集中。
- 迭代过程:在每一步中,将一个群集分割为更小的群集。
- 结束条件:每个数据点成为一个单独的群集,或者达到了预设的群集数量。
案例分享
我们使用的数据集是某一特定购物中心的客户详细信息及其消费得分。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import scipy.cluster.hierarchy as sch
dataset = pd.read_csv('Mall_Customers.csv')
dataset.head()

我们的目标是根据客户的支出得分对客户进行聚类。
X = dataset.iloc[:, [3, 4]].values
dendrogrm = sch.dendrogram(sch.linkage(X, method = 'ward'))
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Euclidean distance')
plt.show()

from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(n_clusters = 5, affinity = 'euclidean', linkage = 'ward')
y_hc = hc.fit_predict(X)
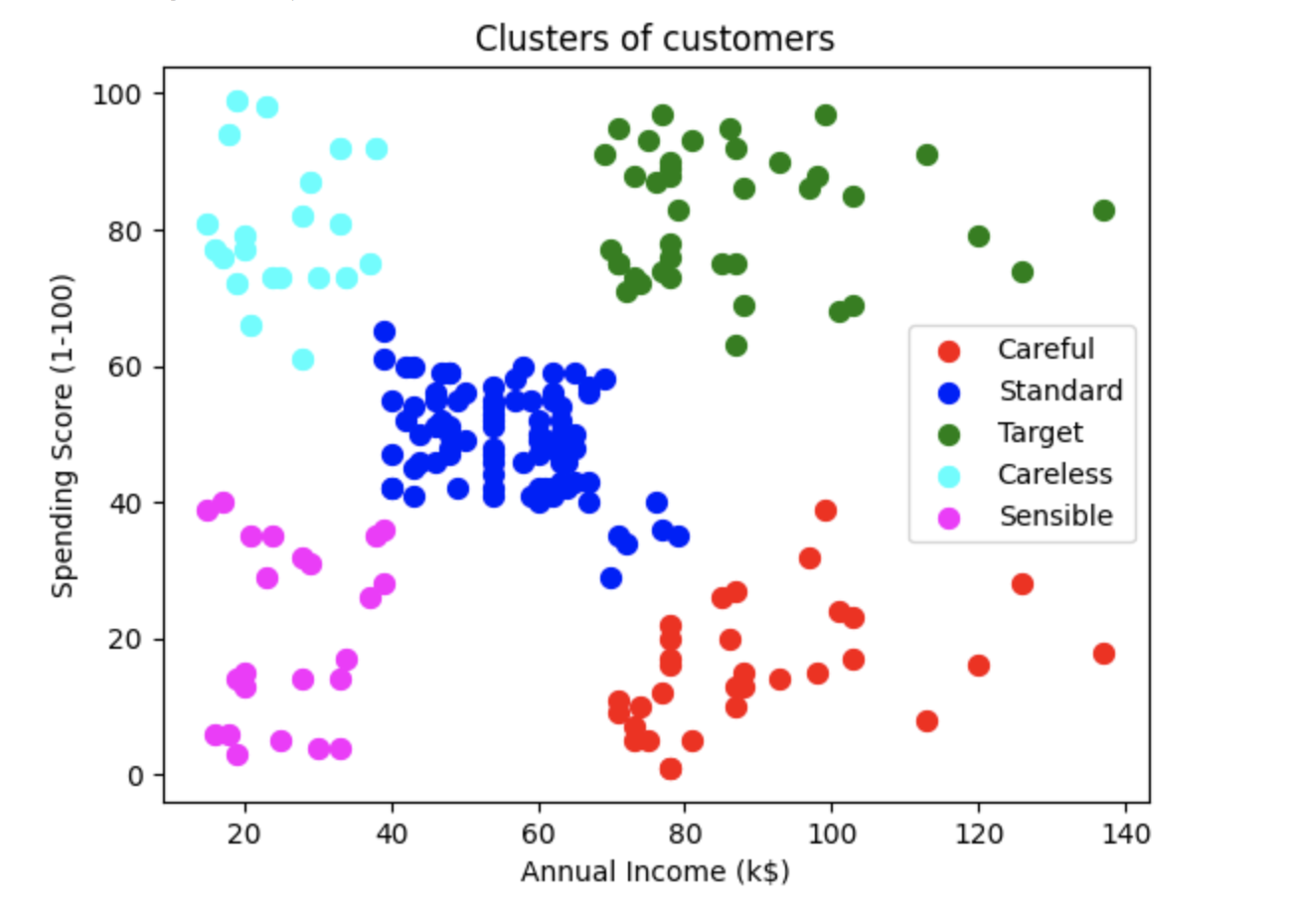
plt.scatter(X[y_hc == 0, 0], X[y_hc == 0, 1], s = 50, c = 'red', label = 'Careful')
plt.scatter(X[y_hc == 1, 0], X[y_hc == 1, 1], s = 50, c = 'blue', label = 'Standard')
plt.scatter(X[y_hc == 2, 0], X[y_hc == 2, 1], s = 50, c = 'green', label = 'Target')
plt.scatter(X[y_hc == 3, 0], X[y_hc == 3, 1], s = 50, c = 'cyan', label = 'Careless')
plt.scatter(X[y_hc == 4, 0], X[y_hc == 4, 1], s = 50, c = 'magenta', label = 'Sensible')
plt.title('Clusters of customers')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()
层次聚类算法中有哪些链接方法?
一些常见的链接方法有:
- 完全链接:两个簇之间的距离定义为每个簇中两点之间的最长距离。
- 单链接:两个簇之间的距离定义为每个簇中两点之间的最短距离。
- 平均链接:两个簇之间的距离定义为一个簇中的每个点到另一个簇中的每个点之间的平均距离。
- 质心链接:找到簇1的质心和簇2的质心,然后计算两者之间的距离。

层次聚类的方法有哪些?
层次聚类主要有两种类型,即 凝聚的层次聚类 和 分裂的层次聚类。
在层次聚类中,"树状图"(Dendrogram)是什么,它如何帮助我们理解数据?
树状图(Dendrogram)是一种图形化的表示方式,用于展示数据的层次聚类结果。
它是层次聚类算法中的一个关键组成部分,因为它提供了一种直观的方式来理解数据点是如何逐步组合成更大的群集的。
在树状图中,Y 轴表示观测值之间的相似度,X 轴表示给定数据集中存在的所有观测值。
对于下面给出的树状图,我们是如何找到最合适的簇数呢?
我们可以通过观察树状图来选择最佳的簇数。
聚类数量的最佳选择是树状图中与水平线相交的垂直线的数量,该水平线可以垂直穿过最大距离而不与聚类相交。
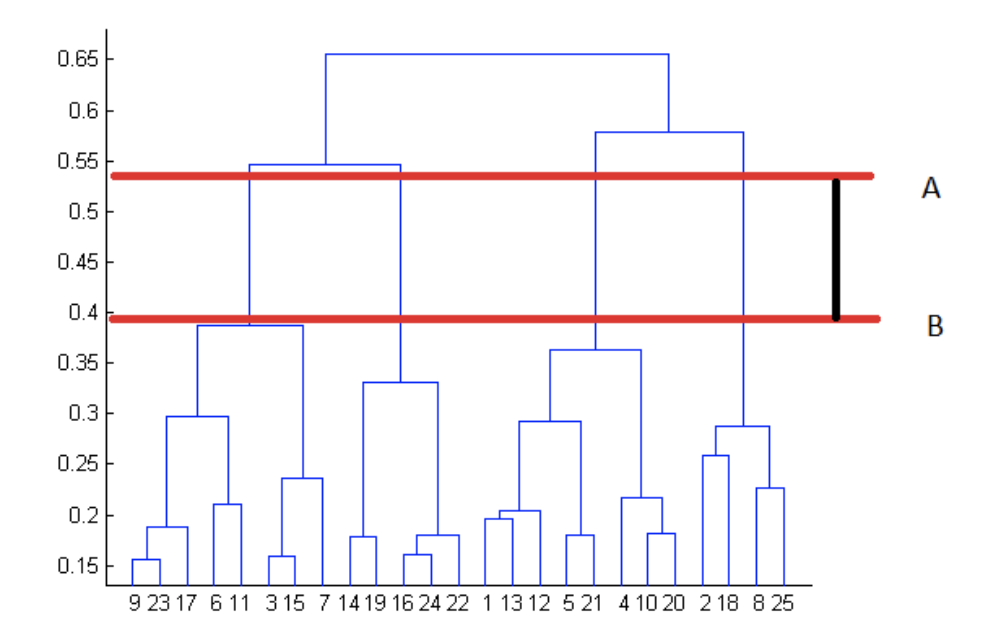
在上面的示例中,簇数的最佳选择为 4,因为下面树状图中的红色水平线覆盖了最大垂直距离 AB。
层次聚类算法的优点和缺点是什么?
优点:
- 我们可以从模型本身获得最佳的聚类数量,不需要人工干预。
- 树状图帮助我们进行清晰的可视化,实用且易于理解。
缺点:
- 由于时间和空间复杂度较高,不适合大型数据集。
- 所有计算簇之间相似度的方法都有其自身的缺点。
层次聚类的局限性和改进方法?
层次聚类的局限性包括。
- 计算复杂度高:传统的层次聚类算法,特别是凝聚的层次聚类(Agglomerative Hierarchical Clustering),其时间复杂度通常为\(O(n^3)\),空间复杂度为 \(O(n^2)\)。这使得它在大规模数据集上效率不高。
可以采用优化的算法,如使用最小生成树(Minimum Spanning Tree)或并行计算来减少计算时间。也可以在数据预处理阶段采用降维技术,比如主成分分析(PCA)减少数据集的规模。
- 对噪声和离群点敏感:层次聚类对噪声和离群点比较敏感,这可能导致不准确的聚类结果。
我们可以在聚类前进行数据清洗,移除或减少噪声和离群点的影响。同时,可以考虑采用基于密度的聚类方法(如DBSCAN),这些方法对噪声和离群点的鲁棒性更强。
- 确定聚类数目困难:在层次聚类中,确定最终聚类的数量通常比较主观,需要用户根据树状图(Dendrogram)来决定。
我们可以采用一些客观的标准来进行改进,如轮廓系数(Silhouette Coefficient),间隙统计(Gap Statistic)或平均轮廓法来帮助确定聚类数目。
