什么是 DBSCAN?

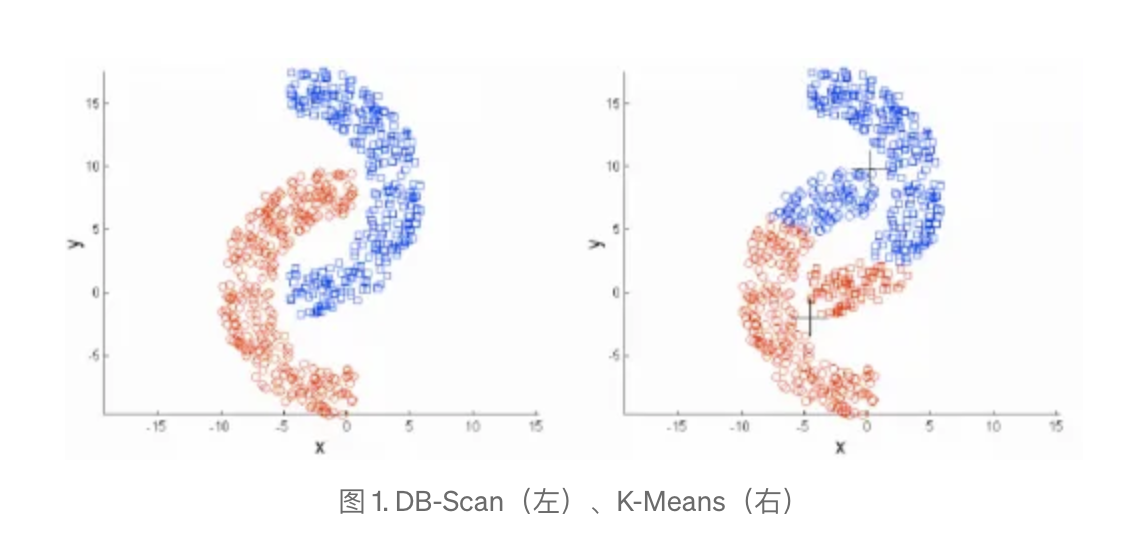
DBScan 是一种基于密度的空间聚类算法，它可以将高密度区域中的点组成一个簇，并能在有噪声的数据集中识别出任意形状的聚类。

DBScan 算法试图将数据空间中紧密相连的点组成一个簇。它不仅能够识别出基于密度的簇，而且能够识别并排除数据中的噪声点。这种基于密度的聚类方法与基于距离的聚类方法（如 K-Means）不同，后者需要事先知道要形成的簇的数量，而且通常只能识别出凸形状的簇。

aaa

DBScan 的优势在于不需要事先指定簇的数量，它可以根据数据本身的结构来确定簇的形成。此外，DBScan 对于数据中的异常值不敏感，因为它不会将噪声点纳入任何簇中。

image-20231109190525741

算法的核心概念

以下是该算法的核心概念。

  1. 密度：该算法基于一个点的 "邻域" 内的点数（即密度）来进行聚类。

  2. ε-邻域：对于任意一个点 p，其 ε-邻域包含了距离 p 小于等于 ε 的所有点。

  3. 核心点：如果一个点的 ε-邻域内至少有 minPts（最小点数参数）数量的点，则该点为核心点。这意味着核心点是在密集区域内的点。

  4. 边界点：如果一个点不是核心点，但它的 ε-邻域内包含至少一个核心点，那么它是边界点。

  5. 噪声点：如果一个点不是核心点也不是边界点，则它被视为噪声点。

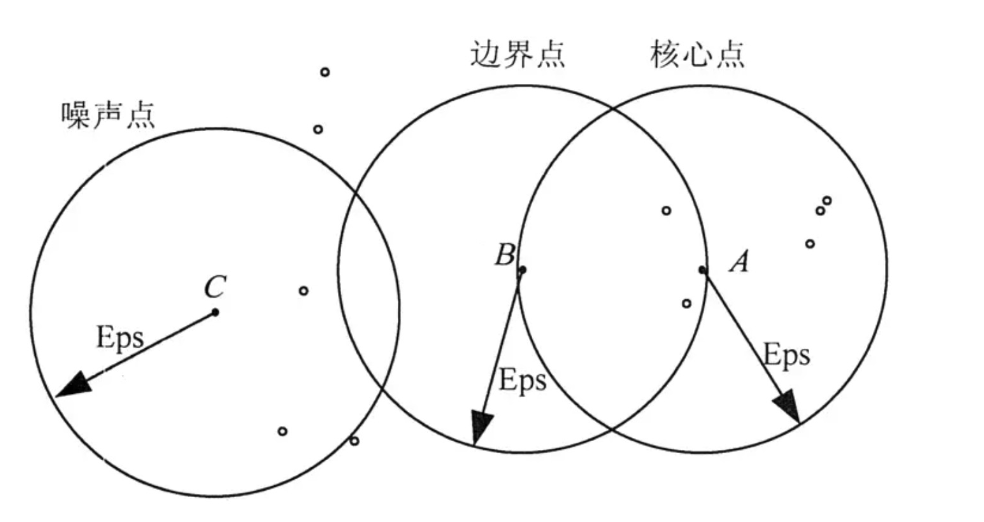
以下图为例，假定最小点数 MmPts=5，则：

  • 点 A 为核心点，其 ε-邻域内超过了5个点；
  • 点 B 为边界点，其 ε-邻域内小于5个点，且落在了点 A 的 ε-邻域内；
  • 点 C 为噪声点，其 ε-邻域内小于5个点，且没有落在任何核心点的邻域内。

image-20240112115811449

  1. 直接密度可达：如果点 q 在点 p 的 ε-邻域内，并且 p 是一个核心点，我们说 q 是从 p 直接密度可达的。

  2. 密度可达：如果存在一个点的序列 p1, p2, ..., pn，其中 p1 是核心点，pi+1 是从 pi 直接密度可达的，那么 pn 是从 p1 密度可达的。

  3. 密度相连：如果存在一个点 o 使得点 p 和 q 都是从 o 密度可达的，那么 p 和 q 密度相连。

算法流程

DBScan 算法的一般步骤如下。

  1. 算法开始时，所有点都标记为未访问。
  2. 对每个未访问的点，以此为中心，计算其 ε-邻域内的所有点。
  3. 如果该点的 ε-邻域内至少有 minPts 数量的点，则创建一个新簇，否则标记该点为噪声（可能在后面步骤中被标记为边界点）。
  4. 如果一个点是核心点，则对其 ε-邻域内的所有未访问点递归地执行相同过程，这会导致簇的扩展。
  5. 这一过程持续进行，直到所有的点都被访问。

aaa

案例分享

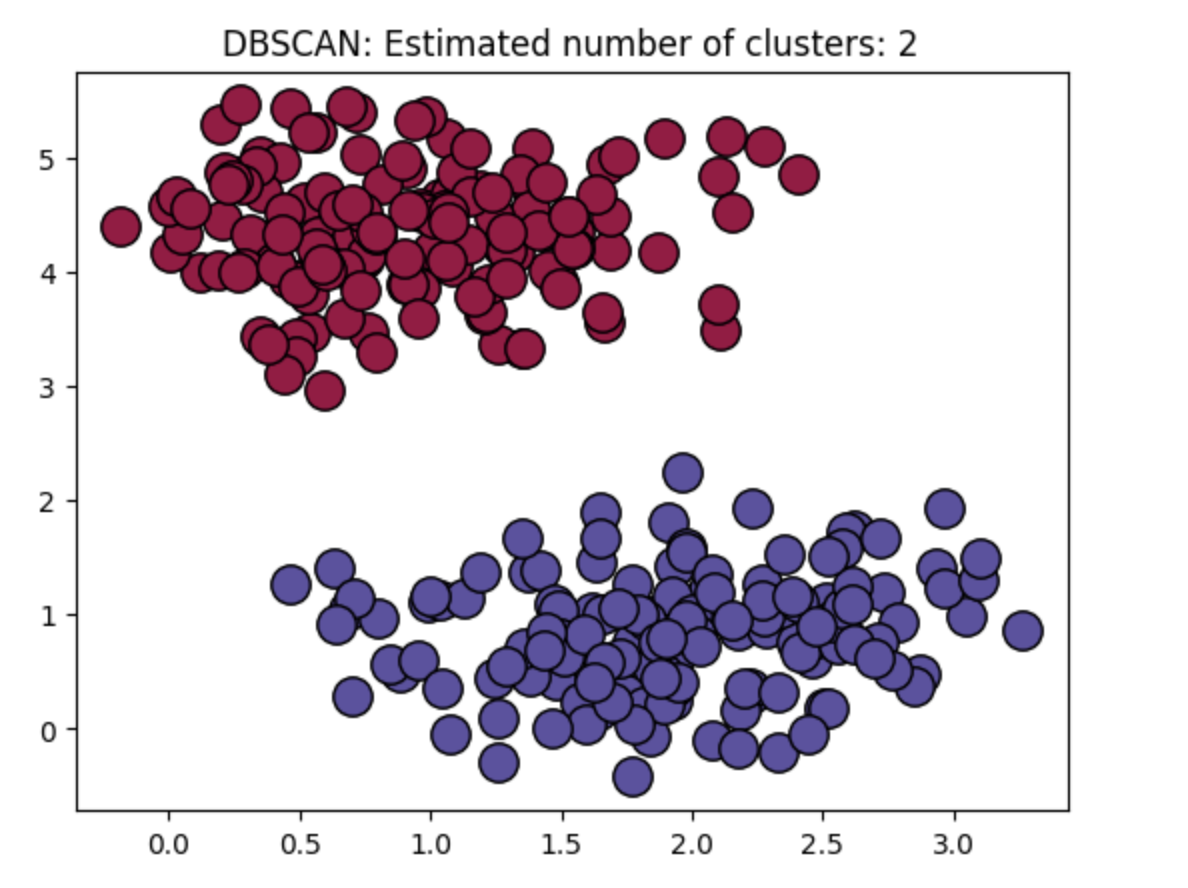
以下是用 Python 实现 DBScan 算法的一个简单例子。

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np

# 生成样本数据
X, _ = make_blobs(n_samples=300, centers=2, cluster_std=0.60, random_state=0)

# 应用DBSCAN算法
db = DBSCAN(eps=0.5, min_samples=5).fit(X)
labels = db.labels_

# 识别核心样本
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True

# 去除噪声数据
X_core = X[core_samples_mask]
labels_core = labels[core_samples_mask]

# 绘制结果
unique_labels = set(labels_core)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]

for k, col in zip(unique_labels, colors):
    if k == -1:
        # 黑色用于噪声
        col = [0, 0, 0, 1]

    class_member_mask = (labels_core == k)

    xy = X_core[class_member_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=14)

plt.title('DBSCAN: Estimated number of clusters: %d' % len(unique_labels))
plt.show()

image-20231109190951241

DBSCAN 如何确定最优的领域半径 ε ？

确定 DBSCAN 算法中最优的领域半径 ε（epsilon）是非常重要的，因为它直接影响着聚类的结果。选择合适的 ε 值需要考虑数据集的特点和密度。

以下是一些常用的方法来确定最优的 ε 值：

K 距离图

K 距离图是确定 ε 值的一种常用方法。这个方法的步骤如下：

  1. 选择一个小的 k 值

通常，k 取决于数据集的大小和密度。一个常用的启动点是 k = sqrt(n)，其中 n 是数据集中的点的数量。

  1. 计算所有点的 k-距离

对于数据集中的每个点，计算它到第 k 近邻的距离。

  1. 绘制 k-距离图

对所有点的第 k 近邻的距离进行排序并绘制成图。横轴是点的索引，纵轴是到第 k 近邻的距离。

  1. 分析图形

K-距离图中的拐点（即图中曲线的急剧上升点）通常被认为是合适的 ε 值。这个拐点表示距离开始显著增加的点。

基于领域内容的方法

另一种方法是通过观察数据点的领域（即在某个 ε 距离内的邻近点）来选择 ε：

  1. 选择一个初始 ε 值：从一个较小的 ε 值开始。
  2. 观察领域内的点数：对每个点，计算在该 ε 距离内的邻近点数量。
  3. 调整 ε 值：如果大多数点的邻近点数量太少或太多，这可能表明 ε 值设定得太小或太大。根据观察结果调整 ε 值，重复此过程。

DBSCAN 如何确定最优的 MinPtS 值？

通常，我们应该将minPts设置为大于或等于数据集的维数。也就是说，我们经常看到人们用特征的维度数乘以2来确定它们的minPts值。

就像用来确定最佳的epsilon值的“肘部方法”一样，minPts的这种确定方法并不是100%正确的。

DBSCAN 算法是如何解决噪声和离群点的？

DBSCAN 的核心思想是基于密度的聚类。算法将密集区域（即邻近点数量超过某个阈值的区域）的点聚集成一个簇。这种方法自然地将数据集中的高密度区域（簇）与低密度区域（噪声或离群点）区分开。

DBSCAN 聚类的优缺点？

优点

  • 不需要预先指定簇的数量，与 K-means 不同，DBSCAN 不需要在聚类前指定簇的数量，这对于对数据集不了解的情况非常有用。
  • 可以发现任意形状的簇，DBSCAN 不仅可以识别凸形状的簇，还可以发现非常复杂和任意形状的簇。
  • 对噪声和异常值有较好的鲁棒性，DBSCAN 能有效地识别并处理噪声数据。
  • 不依赖于距离度量的选择，虽然 DBSCAN 通常使用欧几里得距离，但它可以与任何距离度量一起使用，这使得它在多种类型的数据集上都很有效。

缺点

  • 参数选择难度，虽然参数较少，但正确选择 ε（邻域半径）和 MinPts（最小点数）对于算法的成功至关重要，而且有时很难决定合适的值。
  • 可变的密度问题，如果数据集中的簇具有显著不同的密度，DBSCAN 可能无法很好地识别所有簇。
  • 大规模数据集的处理效率，在处理大规模数据集时，DBSCAN 的计算复杂度可能会变得较高。
  • 边界点的归属问题，在 DBSCAN 中，位于不同簇边界的点可能被分配给任一簇，这可能会导致簇的形状在不同

aaa