大家好，我是小寒

今天给大家分享神经网络中常用的激活函数

激活函数是神经网络中用于将非线性引入模型的数学函数。这种非线性至关重要，因为它允许神经网络学习和表示数据中的复杂关系。

如果没有激活函数，神经网络将仅限于建模线性关系，这会大大降低其在图像识别、语言处理等任务中的有效性。

什么是激活函数

激活函数是人工神经元中的数学函数，它决定是否应该激活（即打开）神经元。

人工神经元对前一层神经元的输入进行线性组合，并应用激活函数来生成最终输出。

它决定特定的神经元对于给定的一组输入是否具有作用（神经元应该是开还是关），以及如果神经元被激活（开），它在输出中起多大作用（激活函数输出的幅度值）。

image-20240703164458677

如上图所示，\(x_{i}\) 是输入，\(w_{i}\) 是与之对应的权重，\(Z = \sum w_i x_i\) 为输入权重之和，函数 f 代表激活函数，将加权和 Z 输入到激活函数中以获得最终输出 Y。

常见的激活函数

下面，我们来看一下神经网络中常用的激活函数。

Sigmoid/Logistic 激活函数

Sigmoid 激活函数是一种常用于神经网络中的激活函数，它将输入值映射到一个 (0, 1) 之间的范围内。

它的公式如下

\[f(x) = \frac{1}{1+e^{-x}}\]

输入值越接近 ∞ ，它就越接近 +1 ，同样，输入值越接近 –∞ ，它就越接近 0 。

image-20240718175241498

image-20240208173448989

sigmoid 函数的优点

  • sigmoid 函数将任意输入值映射到 (0, 1) 之间，这非常适合用来表示概率。因此，它常用于神经网络的输出层，尤其是在二分类问题中。
  • Sigmoid 函数是平滑且连续的，这意味着它在整个输入范围内都有定义和导数。这种性质使得它在优化过程中很容易计算梯度。

Sigmoid 激活函数的局限性

梯度消失问题

sigmoid 函数的导数如下

\[f'(x) = \frac{e^{-x}}{(1+e^{-x})^2} = \frac{1+e^{-x}-1}{(1+e^{-x})^2} = \sigma(x)(1-\sigma(x))\]

从图形上来说，这可以表示为

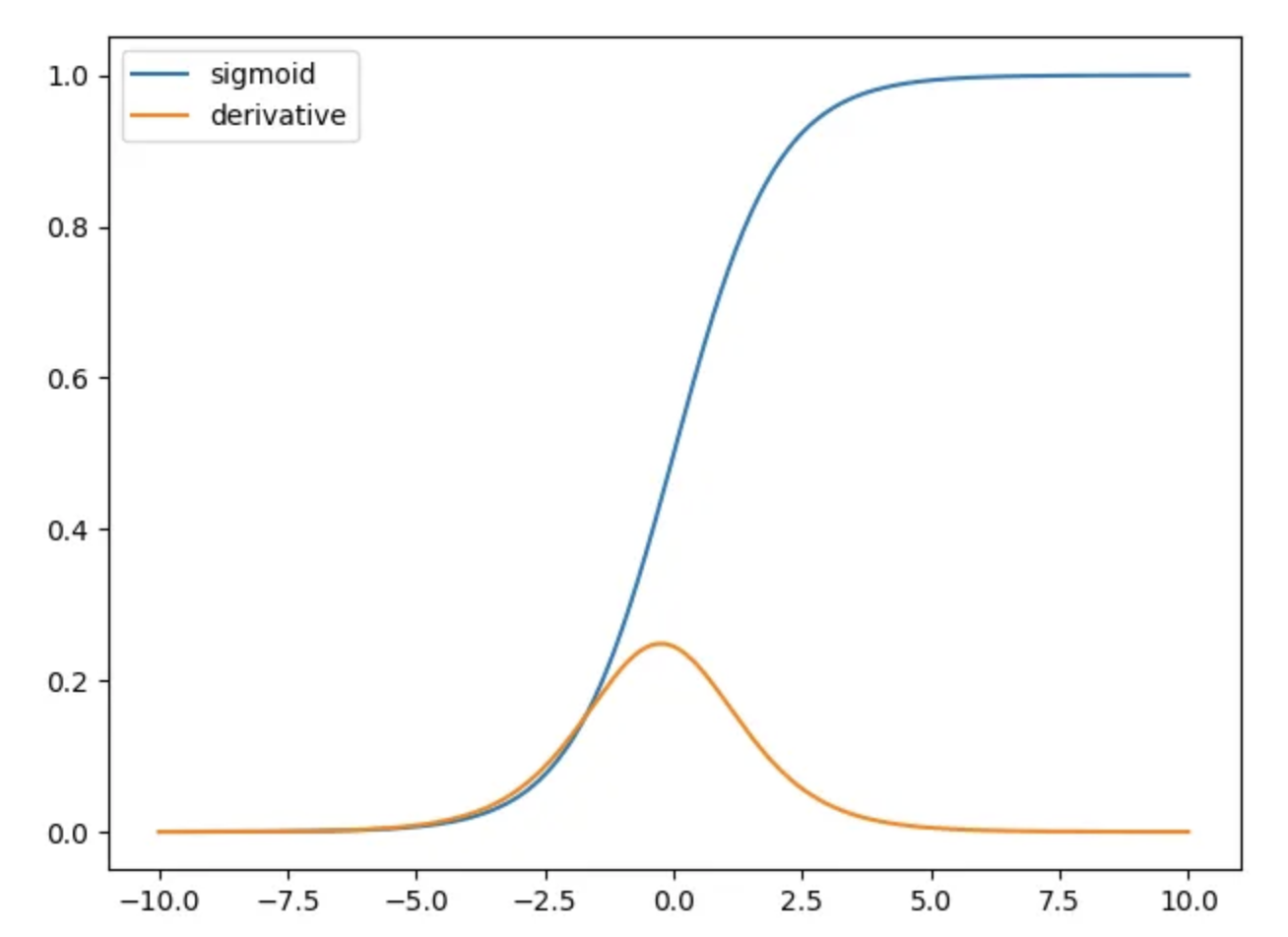
image-20240208173621380

从图中可以看出，梯度值在一定范围（-5.0 到 5.0）之间显着，并且随着进一步增大，图形变得更加平坦。

这表明对于 > 5 或 < -5 的值，该函数将具有较小梯度并最终接近零。这就是神经网络停止学习的地方，因此得名梯度消失。

Tanh 激活函数

sigmoid 函数和 Tanh（双曲正切）函数的区别在于后者将输入值映射到 -1 和 1 之间的范围内。

image-20240718175216602

image-20240208174101610

它表示为

\[f(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}\]

Tanh 函数的优点是

  • Tanh 函数将输入值映射到 (-1, 1) 之间。这与 Sigmoid 函数的 (0, 1) 范围不同，有助于减少网络的偏置效应。
  • 它通常用在神经网络的隐藏层中，因为它的值在 -1 到 1 的范围内，因此数据的平均值接近 0。这有助于使数据居中并使下一层的学习更容易。

Tanh 函数的局限性

梯度消失问题

tanh 函数的导数如下

\[f'(x) = 1 - (\tanh(x))^2\]

从图形上来说，这可以表示为

image-20240208174402180

显然，与 sigmoid 函数类似，Tanh 函数也面临着梯度消失的问题。

ReLU 激活函数

ReLU 激活函数是现代深度学习中最常用的激活函数之一。

image-20240208174618817

它表示为

\[f(x) = \max(0, x)\]

ReLU激活函数的优点

  • ReLU 函数的计算非常简单，只需要比较输入值和 0 的大小，计算复杂度低，适合大规模神经网络的训练。
  • ReLU 在正半轴上的梯度恒为 1，避免了梯度消失问题，有助于深层网络的有效训练。这使得它比 Sigmoid 和 Tanh 函数更适合用于深层神经网络。
  • 由于 ReLU 会将负值部分截断为 0，导致很多神经元在给定的输入下不被激活。这种稀疏性有助于减少模型的复杂度和过拟合风险。

ReLU 激活函数的局限性

ReLU 激活函数的导数如下

\[f'(x) = \begin{cases} 1 & \text{if } x > 0 \\ 0 & \text{if } x \leq 0 \end{cases}\]

从图形上来说，这可以表示为

image-20240208174844404

正如你所看到的，图的负数一侧使梯度值为 0。

因此，某些神经元的权重和偏差在反向传播过程中不会更新。这会导致永远不会被激活的“死亡神经元”。

所有负输入值立即变为 0，这会影响网络拟合和训练数据的能力。

Leaky ReLU

Leaky ReLU 激活函数是 ReLU 函数的一个变体，用于解决 ReLU 函数的 “Dying ReLU” 问题。

Leaky ReLU 在负半轴上引入了一个小的斜率，以确保神经元在接收到负输入时仍然有非零输出。

image-20240208175231613

它表示为

\[f(x) = \max(0.1x, x)\]

参数化 ReLU

参数化 ReLU（PReLU）是一种改进的 ReLU 激活函数，通过引入可学习的参数来调整负半轴的斜率，从而增强模型的表达能力。

它解决了图左半部分梯度减小到 0 的挑战。该函数在函数的负输入上添加斜率，即参数 \(\alpha\)。参数 ReLU 中的反向传播涉及找出最合适的 \(\alpha\) 值。

image-20240208180152997

它表示为

\[f(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha x & \text{if } x < 0 \end{cases}\]

其中，\(\alpha\) 是一个可学习的参数，通常初始化为一个较小的正数。

参数化 ReLU 激活函数的局限性

PReLU 为每个神经元引入一个额外的参数 \(\alpha\)，这会增加模型的参数数量，特别是在大型神经网络中，可能导致模型过拟合的风险增加。如果训练数据不足，过多的参数可能会降低模型的泛化能力。

ELU

该激活函数也是 ReLU 激活函数的变体，其主要目标是修改函数负部分的斜率。

与 Leaky ReLU 和 参数化 ReLU 不同，ELU 使用对数曲线来转换负值。

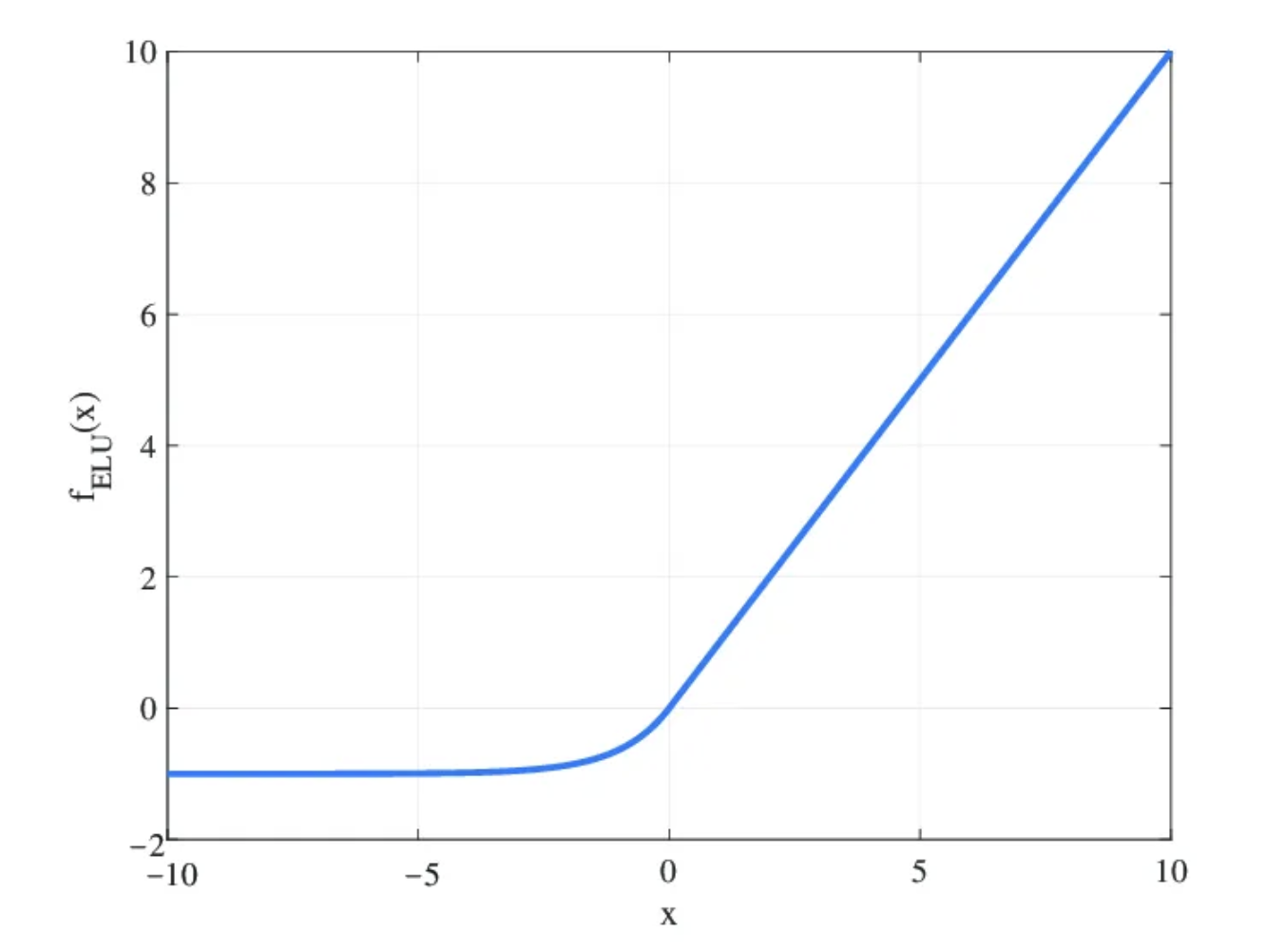
image-20240208180543603

它表示为

\[f(x) = \begin{cases} x & \text{if } x \geq 0 \\ \alpha(e^x - 1) & \text{if } x < 0 \end{cases}\]

ELU 的优点

  • ELU 逐渐平滑，直到输出为 \(-\alpha\)，而 ReLU 则很尖锐。
  • 通过引入负值的对数曲线来消除死亡 ReLU 问题，从而帮助神经网络将权重和偏差引导到正确的路径上。

ELU 激活函数的局限性

  • 相比于 ReLU 和 Leaky ReLU 等简单激活函数，ELU 需要计算指数函数，这增加了计算复杂度和计算时间，特别是在深层网络和大规模数据集上。